浮点数 IEEE 754

二进制科学计数法

公式: -1^sign * mantissa * 2^exponent

浮点数的特点

• 只能精确表示可由二进制科学计数法 (-1)^s * m * 2^e 表示的数值, m 超出精度的部分自动进一舍零. 这也是 0.1, 1.1 等浮点数无法被精确存储的原因

  // 以下使用 JavaScript 实现的双精度浮点数, 精度为 15.95, 约 16 位有效数字 有效数字是指在一个数中，从该数的第一个非零数字算起的所有数字的长度 (0.1).toPrecision(16); // "0.1000000000000000" 对于0.1, 有效数为16位 (0.1).toPrecision(17); // "0.10000000000000001" 对于0.1, 有效数为17位 (0.1).toPrecision(18); // "0.100000000000000006" (0.1).toPrecision(22); // "0.1000000000000000055511" (1.1).toPrecision(16); // "1.100000000000000" 对于1.1, 有效数为16位 (1.1).toPrecision(17); // "1.1000000000000001" 对于1.1, 有效数为17位 (1.1).toPrecision(18); // "1.10000000000000009" (1.1).toPrecision(22); // "1.100000000000000088818" 1.000000000000001; // 控制台输入后值为 1.000000000000001 有效位数为16位 1.0000000000000001; // 控制台输入后值为 1 第17位的1被舍去了

• 规约形式浮点数的最大值: ±(1 + (2^-1 + 2^-2 + ... + 2^-m)) * 2^(2^(e-1) - 1) <=> ±(2 - 2^-m) * 2^(2^(e-1) - 1).
  对于双精度浮点数来说, 其规约最大值为: ±(2- 2^-52) * 2^1023 === ±1.7976931348623157e+308, 1.7976931348623157e+308 也是 JavaScript 中 Number 对象静态属性 MAX_VALUE 的值 (注意它不是一个安全整数), 大于该值即表示 ∞ (Number.MAX_VALUE * 1.000000000000001 === Infinity; Number.MAX_VALUE + 1e+292 === Infinity)

• 非规约形式浮点数的最小值: ±2^(-m + (1 - (2^(e-1) - 1))).
  对于双精度浮点数来说, 其非规约最小值为: ±2^(-52-1022) === ±5e-324, 5e-324 也是 JavaScript 中 Number 对象静态属性 MIN_VALUE 的值, 小于该值即表示 0

• 浮点数的安全整数范围 (安全整数范围指浮点数与整数可以一对一): [-(2^m - 1), 2^m - 1]. 对于双精度浮点数来说, 安全整数为: ±2^53 - 1 === ±9007199254740991, 共有 16 位有效数字. 非安全整数的特点是: 一个浮点数对应多个实数, 如下图所示: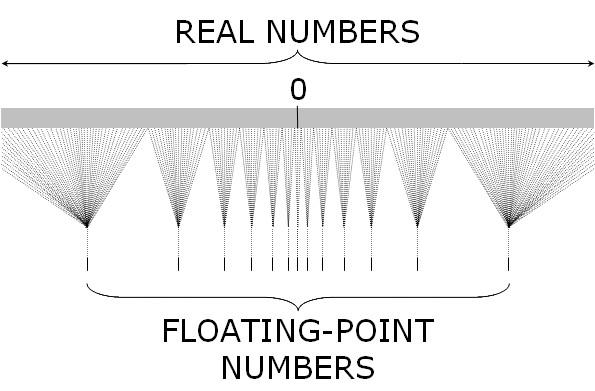

  

  这也是 JavaScript 中 Number 对象静态属性 MAX_SAFE_INTEGER 和 MIN_SAFE_INTEGER 的值
  2^53 + 1 用二进制表示为: 1000...0001 (共 54 位, 两个一分别是 2^{53 和 2}0), 转为二进制科学表示法为: 1.000...0001 * 2^53 (尾数的小数部分共 53 位), 由于双精度浮点数的尾数最多能保存 52 位二进制, 因此最后的 1 注定被舍去. 2^53 + 1 与 2^53 存储一致, 也即 2^53 === 2^53 + 1, 2^53 不是一个安全整数

• 浮点数可以准确表示的整数 (除了安全整数范围内的数), 以双精度浮点数为例: 由于尾数的小数部分最多只能存储 52 位, 因此大于浮点数的安全整数范围并且还要精确表示的整数有两类

  • 一类是在指数的范围内增加指数的大小, 且保持尾数始终为 1.0 的数: 2^54, 2^55, 2^56, ..., 2^1023, 这些都是精确的数

  • 另一类是指数与尾数同时更改的数: 对于 [2^{53, 2}54) 之间的数, 因为其尾数的小数部分共有 53 位, 第 53 位注定会被舍去, 那我们只要保证数的第 53 位为 0, 那么该数即可精确保证, 也即在 [2^{53, 2}54) 之间的偶数才能保证第 53 位为 0, 才能精确表示;

    
    

    同理, [2^{54, 2}55) 之间的数, 第 53 位和第 54 位注定被舍去, 那我们只要保证数的第 53 位和第 54 位都为 0, 那么该数即可精确保证, 也即在 [2^{54, 2}55) 之间, 间距变为 4 的倍数, 这样才能保证第 53 位和第 54 位都为 0, 才能精确表示, 以此类推

浮点数的比较

• 浮点数基本上按照符号位, 指数域, 尾数域的顺序作比较. 显然, 所有正数大于负数; 正负号相同时, 指数的二进制表示法更大的其浮点数值更大; 符号位和指数位相同的, 尾数更大的其浮点数值更大

浮点数的五种舍入方式 (对于二进制浮点数来说是四种舍入方式)

• 舍入到最近的值

  • 舍入到最近的值, roundTiesToEven: 会将结果舍入为最接近且可以表示的值. 如果一样接近, 选择最低有效位为偶数的 (尾数的最低位二进制为 0); 如果最低有效位也相同 (比如 10 进制浮点数 9.5, 9 和 1*e^1 的最低有效位都为奇数), 则选择量级更大的 (对于正数, 越大量级越大; 对于负数, 越小量级越大), 这通常是二进制浮点数的默认舍入方式, 也是十进制浮点数推荐的舍入方式

  // 单精度浮点数(尾数的小数部分23位) Round to nearest, ties to even 示例 // 9.5 表示为二进制科学计数法的浮点数, 舍入一位 9.5 => 1001.1 => 1.0011 * 2^3 // 离它最近的两个数分别为 10 和 9 10 => 1010 => 1.010 * 2^3 9 => 1001 => 1.001 * 2^3 // 10 与 9 离 9.5 的距离分别为 1.010 * 2^3 - 1.0011 * 2^3 = 0.0001 * 2^3 // 0.1 1.0011 * 2^3 - 1.001 * 2^3 = 0.0001 * 2^3 // 0.1 // 距离一样接近, 比较其最低有效位 // 1.010 * 2^3 的最低有效位为 even // 1.001 * 2^3 的最低有效位为 odd // 因此, 9.5 舍入一位后是 10 而不是 9 // 0.95 表示为二进制科学计数法的浮点数, 舍入一位 0.95 => 0.11 1100 1100 1100 1100 1100 1 // 离他最近的两个数分别为 1 和 0.9 1 => 1.00 0000 0000 0000 0000 0000 0 0.9 => 0.11 1001 1001 1001 1001 1001 1 // 1 与 0.9 离 0.95 的距离分别为 1.00 0000 0000 0000 0000 0000 0 - 0.11 1100 1100 1100 1100 1100 1 = 0.00 0011 0011 0011 0011 0011 1 0.11 1100 1100 1100 1100 1100 1 - 0.11 1001 1001 1001 1001 1001 1 = 0.00 0011 0011 0011 0011 0011 0 0.00 0011 0011 0011 0011 0011 1 > 0.00 0011 0011 0011 0011 0011 0 // 0.9 离 0.95 更近一点, 因此 0.95 舍入一位后是 0.9 而不是 1

  • 舍入到最近的值, roundTiesToAway: 会将结果舍入为最接近且可以表示的值. 如果一样接近, 选择量级更大的 (对于正数, 越大量级越大; 对于负数, 越小量级越大), 二进制浮点数不需要该舍入方式, 而十进制浮点数应该提供该舍入方式供用户选择

• 定向舍入

  • 朝 +∞ 方向舍入, roundTowardPositive, 也称为向上取整 ceil: 会将结果朝正无穷大的方向舍入

  • 朝 -∞ 方向舍入, roundTowardNegative, 也称为向下取整 floor: 会将结果朝负无穷大的方向舍入

  • 朝 0 方向舍入, roundTowardZero, 也称为截断 truncation: 会将结果朝 0 的方向舍入

• JavaScript 中 Math.round(x) 静态方法的舍入方式

  • 返回最接近 x 的整数. 如果两个整数相等的接近, 那么返回更接近 +∞ 的; 如果已经是整数了, 那么返回它自身

二进制浮点数的异常处理

• 无效运算, Invalid operation. 数学上未定义的运算, 例如 0/0, sqrt(-1.0) 等, 默认返回 qNaN

• 被零除, Division by zero. 除数为零，被除数为有限的非零数字, 默认返回 ±∞

• 上溢, Overflow. 运算产生的结果超出指数能表达的范围 E max, 默认返回 ±∞

• 下溢, Underflow. 运算产生的结果超出了规约浮点数 normal numbers 的范围, 默认返回非规约浮点数 subnormal numbers 或 0 (遵循舍入规则)

• 不精确, Inexact. 运算产生的结果无法精确表示, 默认返回精确结果的舍入值 (遵循舍入规则)

在线转换 (二进制与十进制) 浮点数的链接

• IEEE-754 Floating Point Converter - Single precision 32-bit

• IEEE754 Single precision 32-bit

• IEEE754 Double precision 64-bit